---

Was ist das Ritterschnittverfahren?

Mit dem Ritterschnittverfahren lassen sich gezielt bestimmte Stabkräfte eines Fachwerks berechnen. Dafür muss ein besonderer Freischnitt gemacht werden, nämlich der Ritterschnitt. Anschließend werden die Gleichgewichts­bedingungen für den Ritterschnitt aufgestellt. Im Gegensatz zum Knotenschnitt­verfahren lassen sich mit dem Ritterschnittverfahren nur einzelne Stabkräfte berechnen.

---

Aufgabe: Stabkräfte berechnen

Das abgebildete Fachwerk ist fest-losgelagert und wird mit drei Kräften \( F_1,\,F_2,\,F_3 \) belastet. Zu berechnen sind die Auflagerkräfte des Systems sowie die Stabkräfte der Stäbe 1, 2 und 4 mithilfe eines Ritterschnitts.

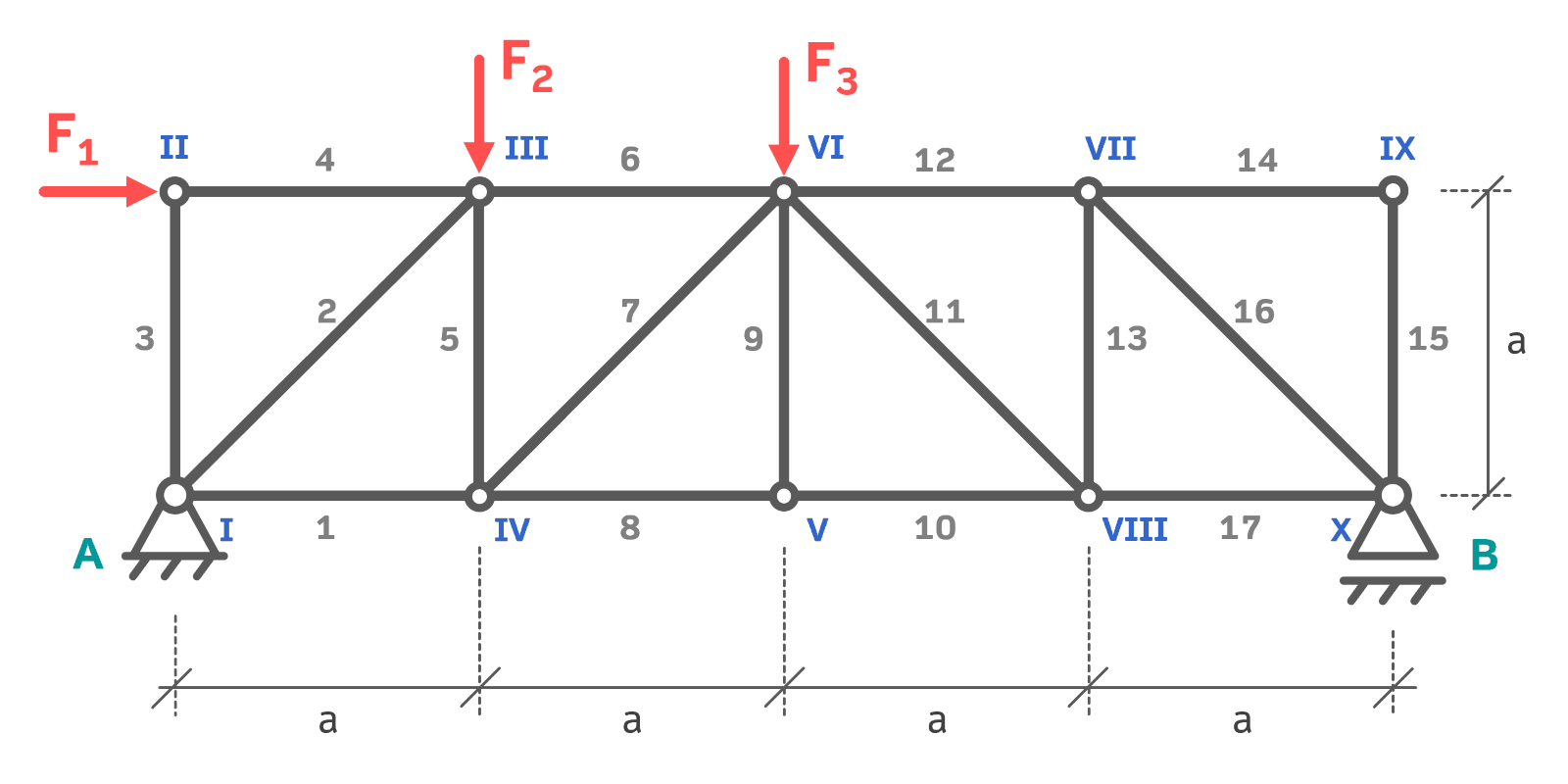
Gegeben: \( F_1=36\,kN,\,F_2=12\,kN,\,F_3=24\,kN,\,a=2\,m \)

---

Lösung per Ritterschnitt

Wir beginnen zuerst mit den Lagerkräften des Systems. Anschließend wird der Ritterschnitt durch die gesuchten Stäbe gesetzt, um die Stabkräfte zu berechnen.

Schritt 1: Auflagerkräfte berechnen

Um mit dem Ritterschnitt die Stabkräfte zu berechnen, muss man meistens die Lagerkräfte kennen (auch ohne, dass die Aufgabenstellung die Auflagerkräfte verlangt). Wir schneiden wie gewohnt das Fachwerk frei (Freikörperbild). Aus den Gleichgewichtsbedingungen erhalten wir die Auflagerkräfte. Die Lagerkräfte dieses Systems wurden im Rahmen einer Übungsaufgabe zum Thema Knotenpunktverfahren berechnet. Wir können sie daher als gegeben annehmen.

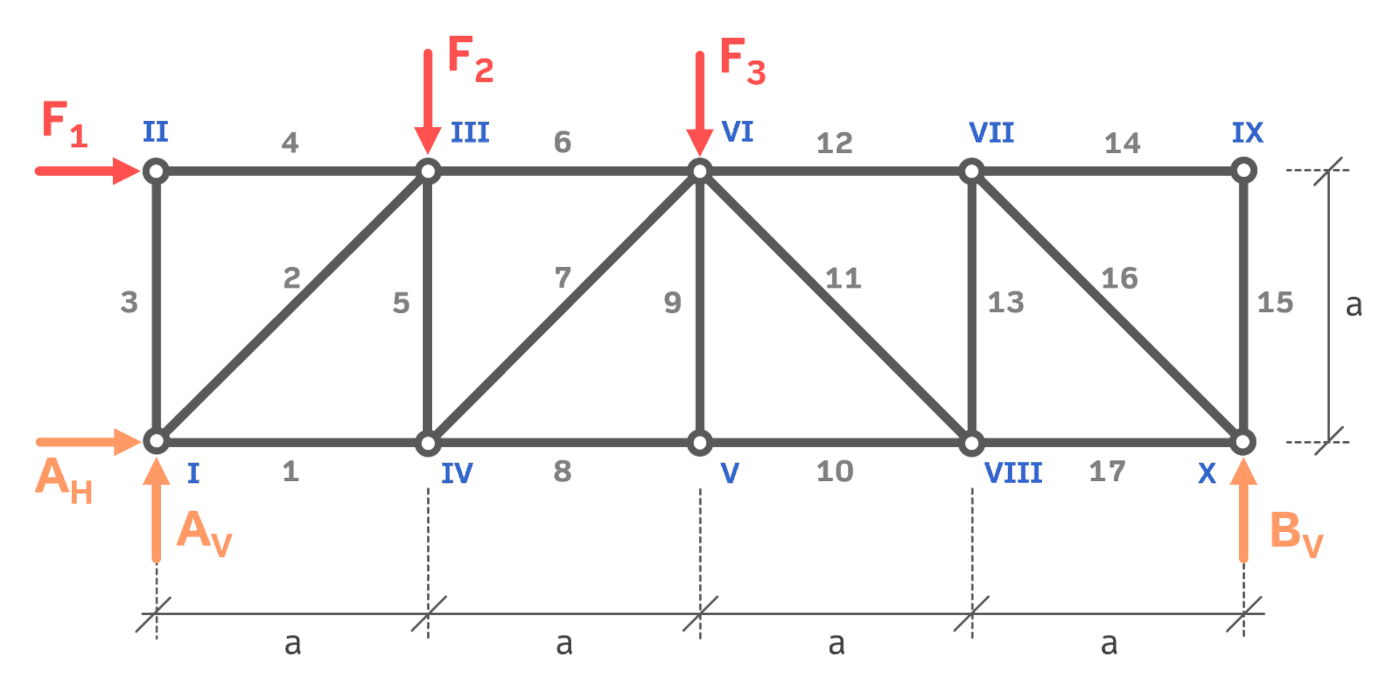
$$A_H=-36\,kN$$ $$A_V=12\,kN$$ $$B_V=24\,kN$$

Schritt 2: Ritterschnitt durch 3 Stäbe

Das Ritterschnittverfahren besagt, dass durch drei Stäbe geschnitten werden muss. Die gesuchten drei Stäbe erfüllen die Bedingungen für den Ritterschnitt. Wir können daher durch die gesuchten Stäbe schneiden:

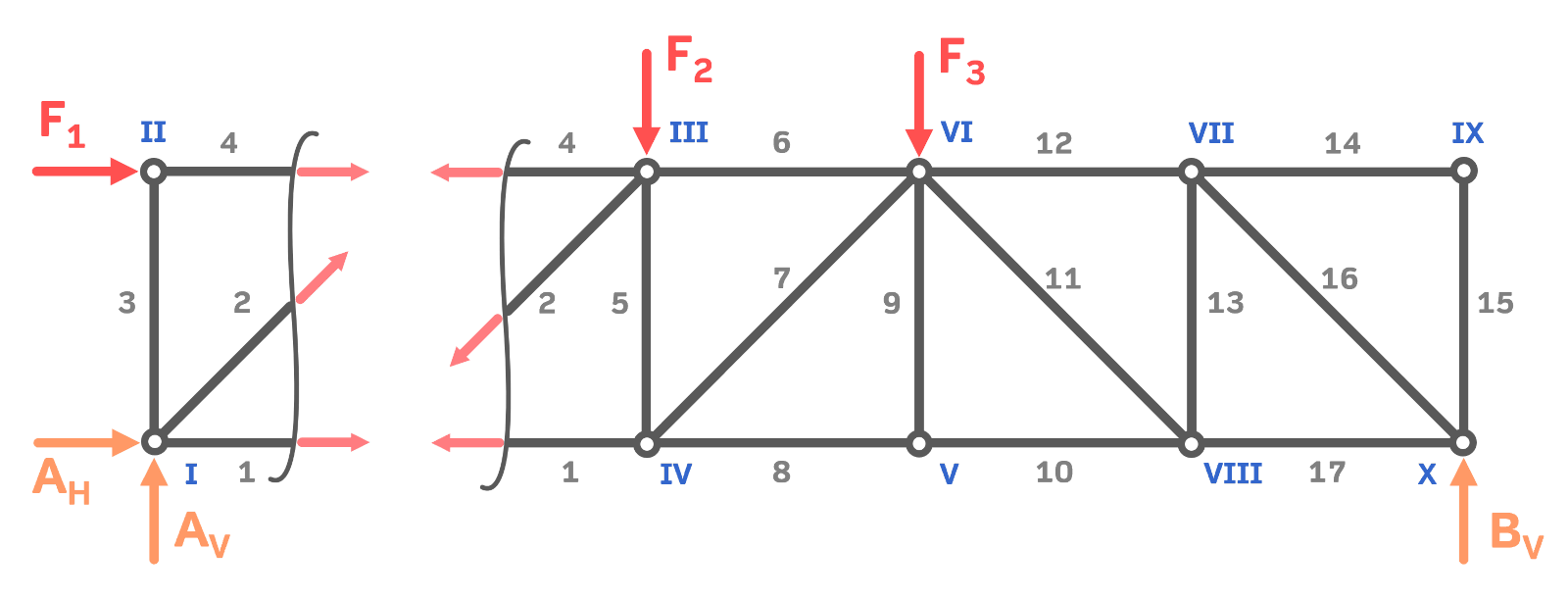
Wie man gut erkennen kann, teilt der Ritterschnitt das Fachwerk in zwei Teile. Der Schnitt durch die Stäbe lässt die gesuchten Stabkräfte außerdem sichtbar werden. Für die Berechnung machen wir mit dem linken Teil des Fachwerks weiter.

Ritterschnitt: linke Seite

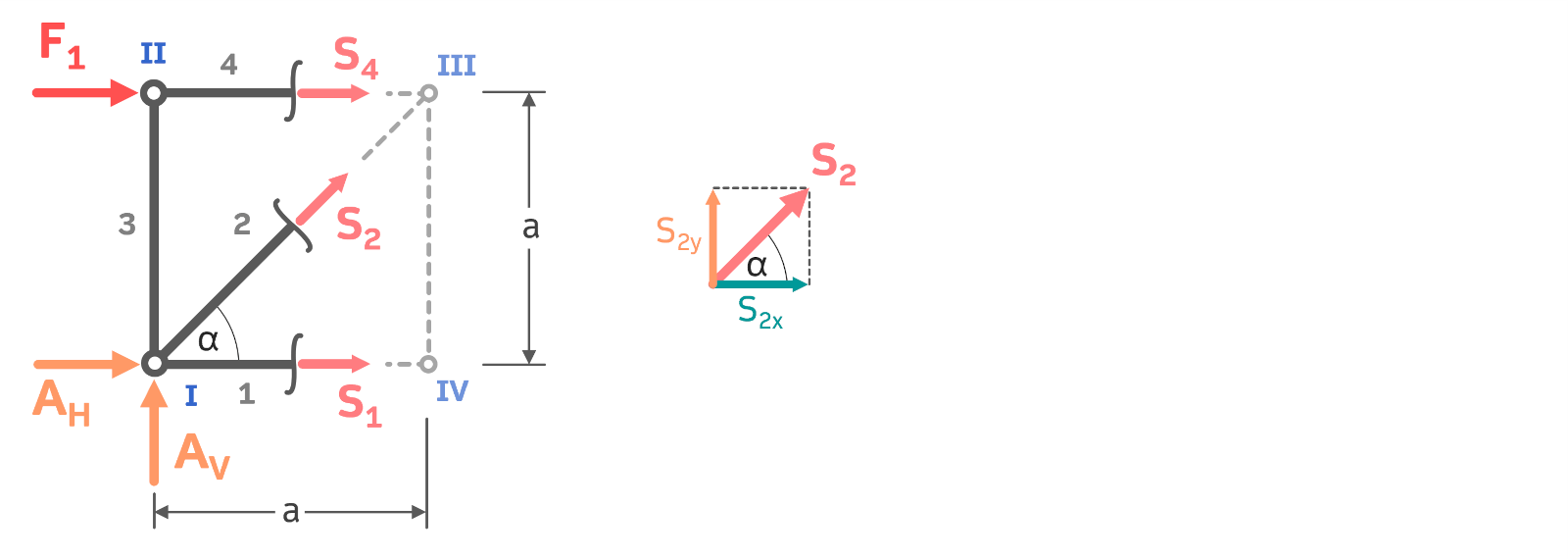
Zum Freikörperbild des Ritterschnitts gehören die Stabkräfte sowie relevante Längen- und Winkelangaben. In diesem Freikörperbild wurden außerdem die benachbarten Knoten III und IV angedeutet. Auf den Knotenpunkt III zeigen zwei unbekannte Stabkräfte: \( S_2,\,S_4 \). Nutzt man diesen Kontenpunkt für eine Momentengleichung, dann fallen diese beiden Stabkräfte raus und man erhält \( S_1\). Gleiches Prinzip auch für Knotenpunkt I:

Summe aller Momente um Knoten III:
$$\sum M^{III}=0=S_1 \cdot a+A_H \cdot a-A_V \cdot a$$ $$\Rightarrow S_1=A_V-A_H=48\,kN$$

Summe aller Momente um Knoten I:
$$\sum M^I=0=-S_4 \cdot a-F_1 \cdot a$$ $$\Rightarrow S_4=-F_1=-36\,kN$$

Die übrig gebliebene Stabkraft \( S_2\) erhält man beispielsweise mit dem Kräftegleichgewicht in x- oder y-Richtung. Da die Stabkraft schräg wirkt, muss sie zunächst zerlegt werden (Kräftezerlegung (Grundlagen)). Rechts neben dem Ritterschnitt ist das Krafteck für die Stabkraft \( S_2\) dargestellt:

$$sin(\alpha)=\frac{S_{2y}}{S_2}\,\Rightarrow S_{2y}=S_2 \cdot sin(\alpha)$$

Den Winkel \( \alpha \) erhält man mit dem Tangens und dem rechtwinkligen Dreieck, das aus den Stäben 1, 2 und 5 besteht (siehe Fachwerk Aufgabenstellung):

$$tan(\alpha)=\frac{a}{a}=1\,\Rightarrow \alpha=45°$$

Nun lässt sich das Kräftegleichgewicht in y-Richtung aufstellen:
$$\sum F_V=0=A_V+S_{2y}$$ $$\Rightarrow S_{2y}=S_2 \cdot sin(\alpha)=-A_V$$ $$S_{2y}=-\frac{A_V}{sin(\alpha)} \approx -16,97\,kN$$

Stab 2 ist somit ein Druckstab (negatives Vorzeichen), ebenso wie Stab 4. Stab 1 hingegen ist ein Zugstab (positives VZ). Die Ergebnisse sind in der folgenden Tabelle zusammengefasst:

\[
\begin{array}{|c|c|c|}
\hline
Stab & Stabkraft\,[kN] & Zug/Druck \\
\hline
1 & 48 & Z \\
\hline
2 & -16,97 & D \\
\hline
4 & -36 & D \\
\hline
\end{array}
\]

---

FAQ: Ritterschnittverfahren

Kann man auch den rechten Teil des Fachwerks wählen?

Gute Frage! Ja, kann man. Das führt zwar zu denselben Ergebnissen. Allerdings ist in diesem Rechenbeispiel der rechte Teil deutlich “komplizierter”. Warum also nicht den leichten und sicheren Weg gehen?

Was ist mit den Nullstäben?

Ausgezeichnete Frage! Natürlich macht es Sinn, vorher die offensichtlichen Nullstäben zu identifizieren. Sollte sich rausstellen, dass einer der gesuchten Stäbe ein Nullstab ist, dann darf das natürlich verwendet werden. Nullstäbe erkennen: Nullstab-Regeln

Spielt es eine Rolle, wie ich die Stabkräfte im Schnitt einzeichne?

Gute Frage! Ja, es spielt eine Rolle. In der Technischen Mechanik hat man sich darauf geeinigt, Stabkräfte so einzuzeichnen, dass sie vom Schnitt wegzeigen. Das ist praktisch, damit man Zugstäbe von Druckstäbe unterscheiden kann. Das Freikörperbild wäre also falsch, wenn die Stabkräfte nicht in die vorgesehene Richtung zeigen.

Wann Zugstab und wann Druckstab?

Ausgezeichnete Frage! Durch die Konvention, dass Stabkräfte stets vom Knoten bzw. vom Schnitt wegzeigen, wissen wir: Ein Stab ist ein Zugstab, wenn das Ergebnis positiv ist. Ein Stab ist ein Druckstab, wenn das Ergebnis negativ ist.

---

Video: Fachwerke berechnen

Stabkräfte berechnen: Dieses Video zeigt Schritt für Schritt, wie Stabkräfte berechnet werden und wie man Nullstäbe identifiziert.

---

Zusammenfassung Ritterschnittverfahren

1. Lagerkräfte berechnen
2. Ritterschnitt durch 3 Stäbe setzen und Freikörperbild zeichnen
3. Drei Gleichgewichtsbedingungen aufstellen und anschließend
4. Drei gesuchte Stabkräfte aus den drei Gleichgewichten berechnen

Tipp: Beim Ritterschnitt kann man oft zwei Momentengleichgewichte aufstellen (so wie es hier gemacht wurde). Das erleichtert die Berechnung der Stabkräfte. Zum Vergleich kann man zu Übungszwecken dieselben Stabkräfte mit zwei Kräftegleichgewichten und einem Momentengleichgewicht berechnen.

---

Verwandte Themen

Stabkräfte berechnen mit dem Knotenpunktverfahren
Nullstäbe erkennen mit den Nullstab-Regeln
Kräftezerlegung: Theorie und Übungsbeispiel
Oder zurück zur Themenübersicht: Technische Mechanik 1