Streckenlast berechnen: Formeln und Überblick
Hier lernst du die wichtigsten Grundlagen zum Thema Streckenlast berechnen: Formeln, Einheit der Streckenlast sowie die Resultierende (resultierende Kraft) einer Streckenlast und ihr Angriffspunkt. Es werden die wichtigsten Streckenlasten vorgestellt: Gleichstreckenlast, Dreieckslast, Trapezlast.
Was versteht man unter einer Streckenlast?
Eine Streckenlast ist eine verteilte Last. Das bedeutet, dass die Last nicht punktuell angreift, sondern über eine Länge verteilt wirkt. Steht eine Person auf einem Trampolin, dann wirkt das gesamte Körpergewicht beinahe punktuell auf die Sprungfläche. Dies entspricht einer Einzellast \( F \). Das Resultat davon ist ein tiefes Absinken der Sprungfläche. Liegt dieselbe Person hingegen auf dem Trampolin, dann wirkt das Körpergewicht verteilt über die Körperlänge auf die Sprungfläche. Dies entspricht einer Streckenlast \( q_0 \). Das Resultat davon ist ein geringes Absinken. Die Einheit der Streckenlast ist \( [q]= \frac{N}{m} \).
Tabelle der wichtigsten Streckenlasten
| Streckenlast | Resultierende Kraft | Gleichung der Streckenlast |
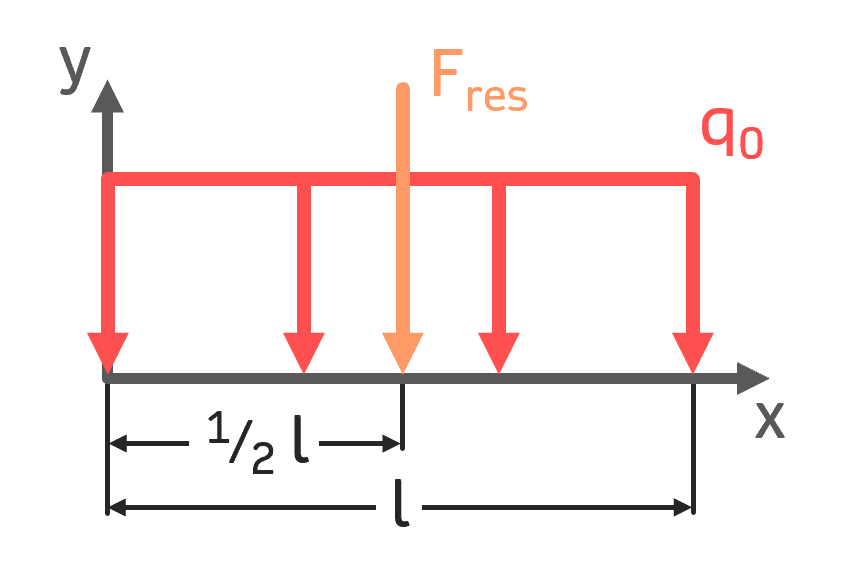 Gleichstreckenlast Gleichstreckenlast |
$$ F_{res} = q_0 \cdot l $$ $$ x_S = \frac{1}{2}\,l $$ | $$ q(x)=q_0 $$ |
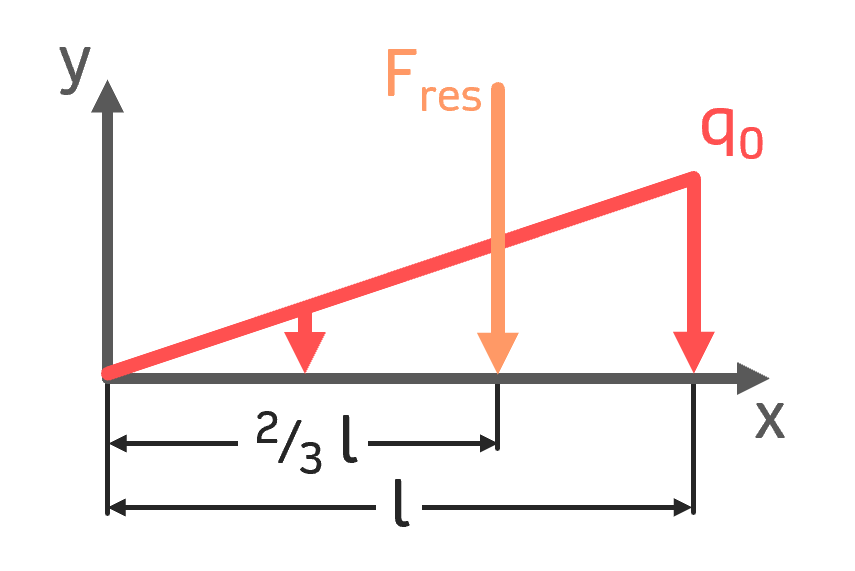 Dreieckslast (zunehmend) Dreieckslast (zunehmend) |
$$ F_{res} = \frac{1}{2} q_0 \cdot l $$ $$ x_S = \frac{2}{3}\,l $$ | $$ q(x)=\frac{q_0}{l} \cdot x $$ |
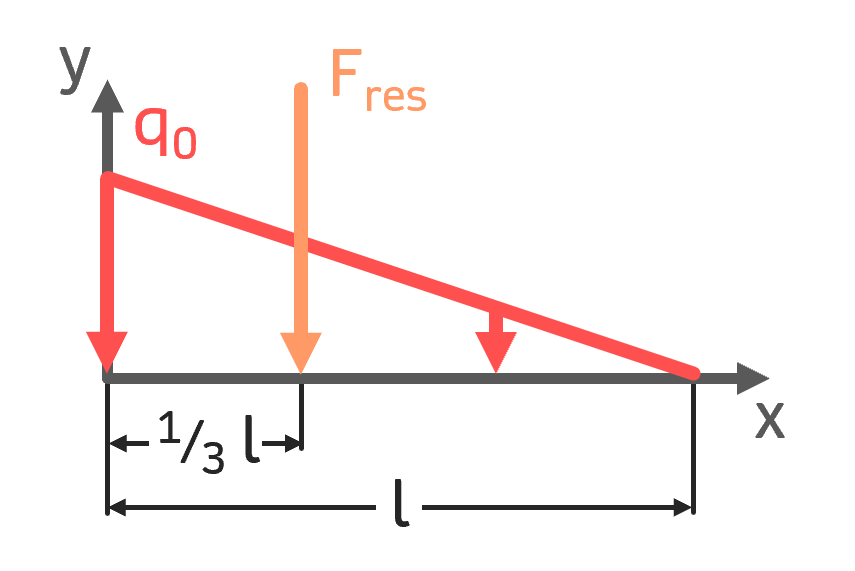 Dreieckslast (abnehmend) Dreieckslast (abnehmend) |
$$ F_{res} = \frac{1}{2} q_0 \cdot l $$ $$ x_S = \frac{1}{3}\,l $$ | $$ q(x) = q_0 – \frac{q_0}{l} \cdot x $$ |
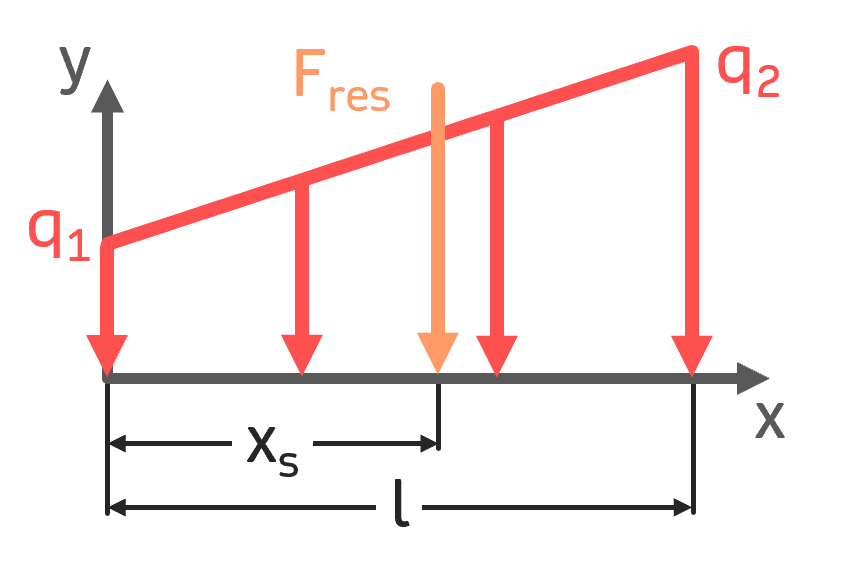 Trapezlast Trapezlast |
$$ F_{res} = \frac{q_1+q_2}{2} \cdot l $$ $$ x_S = \frac{q_1+2q_2}{3(q_1+q_2)} \cdot l $$ | $$ q(x)=q_1+ \frac{q_2-q_1}{l} \cdot x$$ |
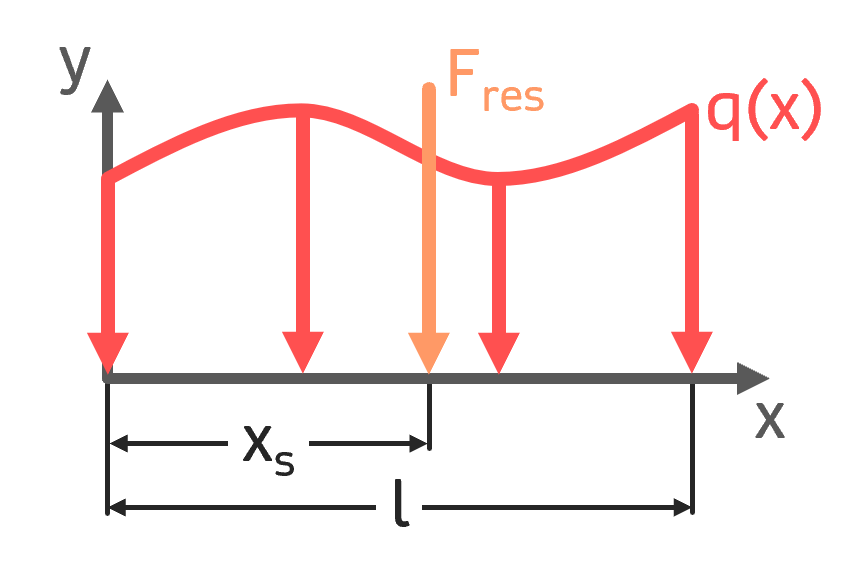 Streckenlast (allgemein) Streckenlast (allgemein) |
$$ F_{res} = \int_{0}^{l} q(x)\,dx $$ $$x_S = \frac{\int_{0}^{l} q(x)\cdot x \,dx}{\int_{0}^{l} q(x)\,dx}$$ | $$ q(x) $$ |
Diese Tabelle steht dir auch als pdf-Datei kostenlos zum Download zur Verfügung: Technische Mechanik 1 Formelsammlung
FAQ: Streckenlast berechnen
Wie berechnet man die Streckenlast?
Um die Streckenlast zu berechnen benötigt man zunächst den Betrag der resultierenden Kraft. Der Betrag gibt an, wie „stark“ die Streckenlast ist und entspricht immer dem Flächeninhalt der Streckenlast:
$$ F_{res} = \int_{0}^{l} q(x)\,dx $$
Für bestimmte Streckenlasten (Gleichstreckenlast, Dreieckslast etc.) ist das Integrieren nicht notwendig, weil die obige Tabelle mit Beispielen genutzt werden kann. Ausführliches Rechenbeispiel mit einer Streckenlast:
Lagerkräfte berechnen: Prüfungsaufgabe
Wie wird der Angriffspunkt der resultierenden Kraft einer Streckenlast berechnet?
Man kann den Angriffspunkt der resultierenden Kraft einer Streckenlast wie folgt berechnen:
$$ x_S = \frac{\int_{0}^{l} q(x)\cdot x \,dx}{\int_{0}^{l} q(x)\,dx} $$
Auch hier bei dem Kraftangriffsort ist es besser, die obige Tabelle mit den Streckenlast Beispielen zu verwenden. Neben dem Betrag der Resultierenden und dem Angriffsort der resultierenden Kraft ist es hin und wieder notwendig, die Gleichung der Streckenlast zu bestimmen. Auch hierfür stehen in der obigen Tabelle die Gleichungen der häufigsten Streckenlast-Typen zur Verfügung.
Wirkt die Streckenlast anders als die Einzellast?
Bleiben wir bei dem anfangs erwähnten Beispiel mit dem Trampolin: Eine Person mit konstantem Gewicht verursacht, je nachdem ob sie steht oder liegt, ein tiefes oder ein geringes Absinken der Sprungfläche. Dieses Beispiel zeigt, dass die Einzellast eine größere Verformung verursacht als die Streckenlast. Die Antwort auf die Frage lautet damit: Ja, die Streckenlast wirkt anders auf das Bauteil. Damit ist die Streckenlast „besser“ für das Bauteil, weil die Belastung verteilt einwirkt und so wenig Verformung und wenig Schaden verursacht. Für die Lagerkräfte hingegen spielt es keine Rolle, ob die Person liegt oder steht. Die Beine des Trampolins (also die Auflager) müssen so oder so das Körpergewicht tragen.
Video zum Thema Streckenlast berechnen
In diesem Video wird Schritt für Schritt erklärt, wie man die Streckenlast berechnen kann. Dabei geht es um einen Balken, der unter anderem mit einer Streckenlast belastet wird.
Verwandte Themen
Formelsammlung: Technische Mechanik 1 (pdf-Download)
Schnittgrößen berechnen: Prüfungsaufgabe
Flächenschwerpunkt: Überblick und Formeln
Oder zurück zur Themenübersicht: Technische Mechanik 1