Schwerpunkt berechnen: Prüfungsaufgabe
Auf dieser Seite lernst du ganz einfach, wie der Flächenschwerpunkt zusammengesetzter Körper berechnet wird. Dafür wird in dieser Aufgabe der Schwerpunkt einer zusammengesetzten Fläche einmal mit der Formel für den Schwerpunkt und einmal mit der Tabelle (Tabellenverfahren) Schritt für Schritt berechnet.
Was ist der Schwerpunkt?
Der Schwerpunkt befindet sich dort, wo man seinen Zeigefinger am Körper positionieren müsste, um ihn im Gleichgewicht zu halten bzw. um diesen zu balancieren.
Aufgabe: Schwerpunkt berechnen
Die abgebildete Fläche setzt sich aus einem Quadrat zusammen, der eine kreisförmige Bohrung und eine dreieckige Aussparung hat. Die Lage des Schwerpunktes der zusammengesetzten Fläche ist zu bestimmen. Das vorgegebene Koordinatensystem ist zu verwenden.
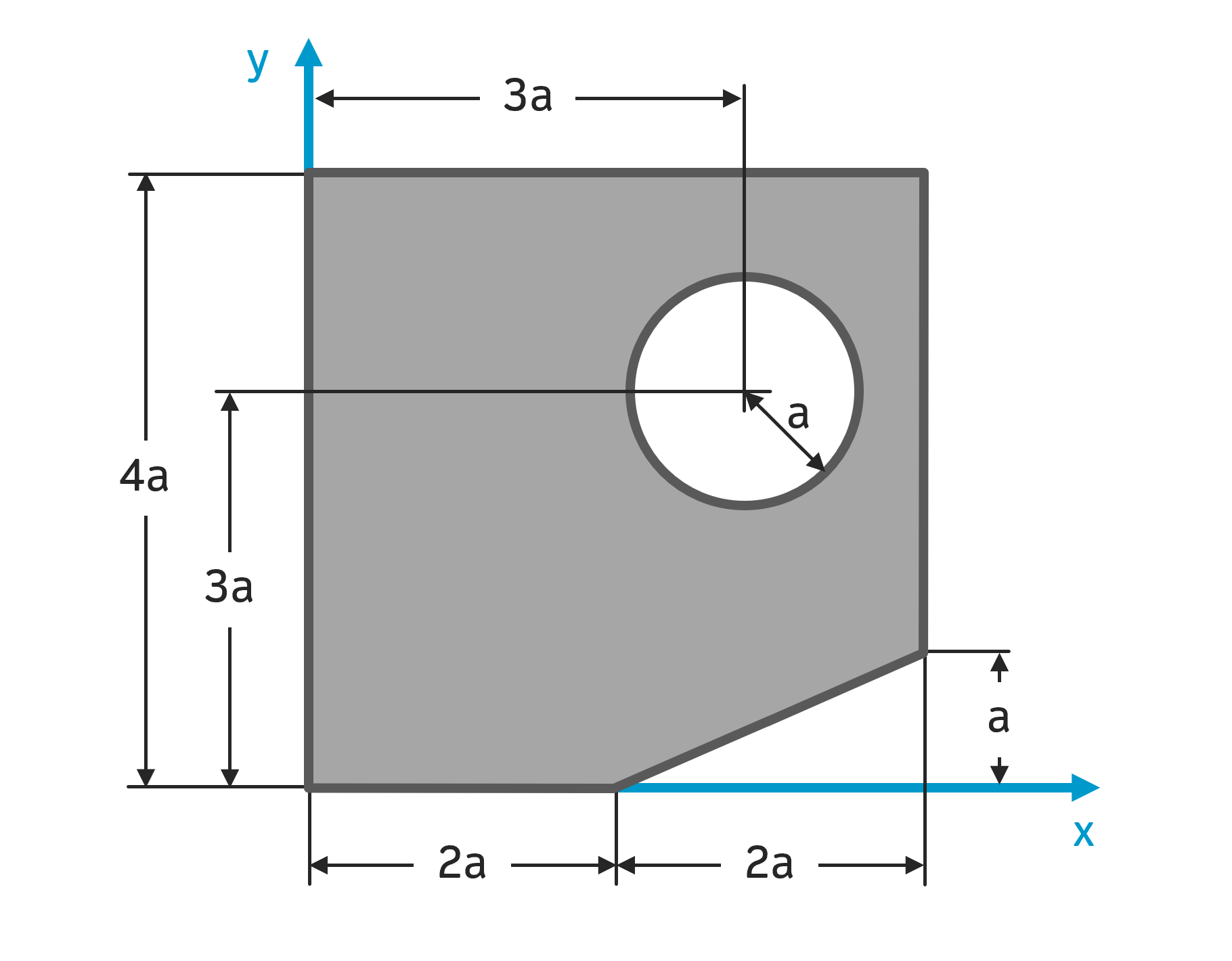
Gegeben: \( a=10\,cm \)
Lösung
Schritt 1: Teilflächen erkennen und nummerieren
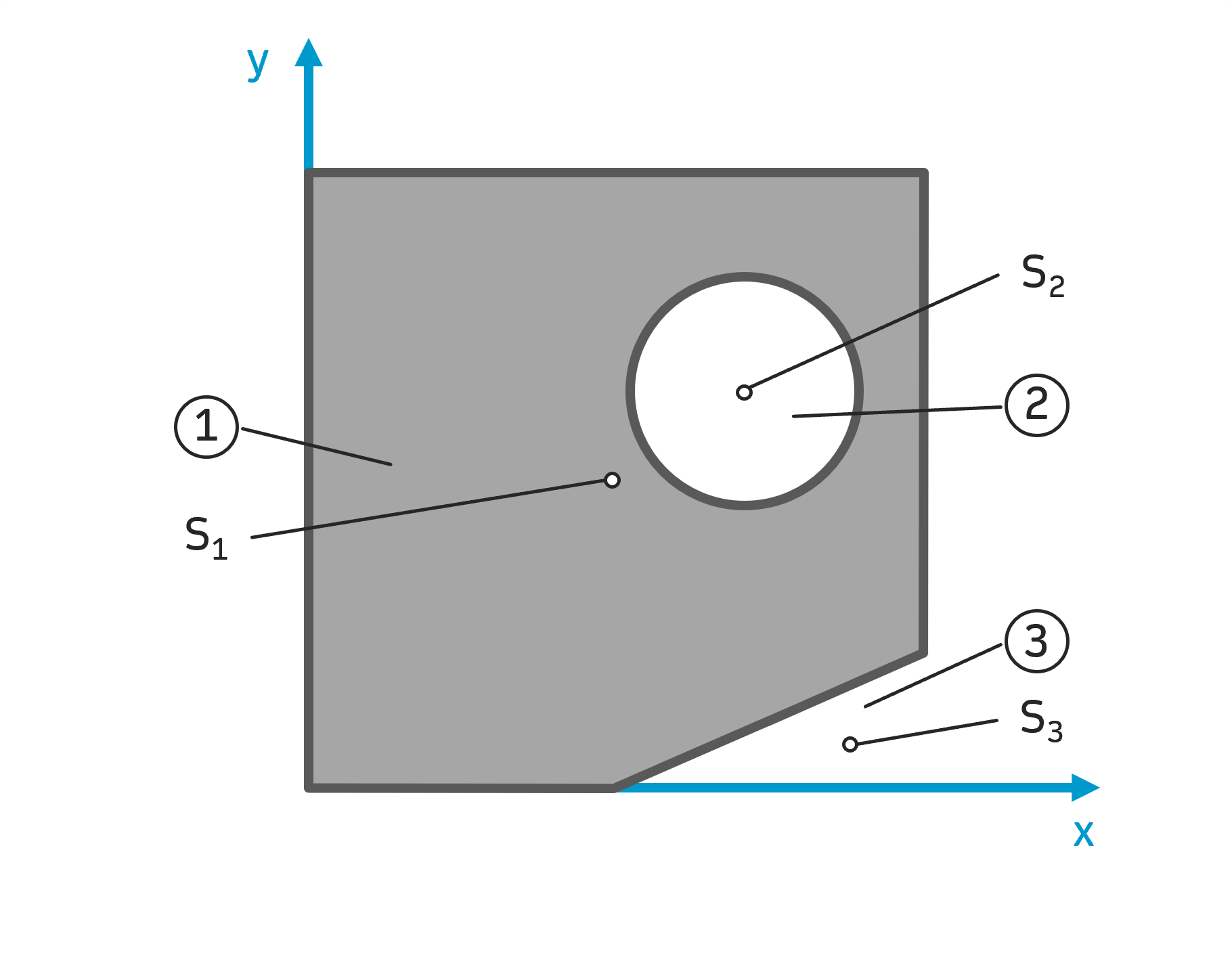
Als erstes sollte man die einzelnen Teilflächen der Gesamtfläche erkennen. Oft setzt sich die Fläche aus Rechtecken, Dreiecken und Kreisen zusammen. Daher Augen auf bei diesen drei Formen. Die Tabelle mit den Schwerpunkten der wichtigsten Flächen kann dir dabei helfen: Flächenschwerpunkt: Überblick und Formeln. In dieser Aufgabe setzt sich die Gesamtfläche aus einem ein Quadrat \( 1 \), einem Kreis \( 2 \) und einem Dreieck \( 3 \) zusammen. Die Nummerierung ist wichtig, damit man später in der Rechnung die einzelnen Flächen voneinander unterscheiden kann (\( A_1\,,A_2\, \) usw.). Außerdem sollte man an dieser Stelle die Lage des Schwerpunktes der einzelnen Teilflächen markieren und mit \( S_1\,,S_2\,,S_3 \) kennzeichnen. Da die Teilflächen ausschließlich aus einfachen Flächen bestehen, ist es kein Problem sein, die jeweiligen Schwerpunktskoordinaten zu finden.
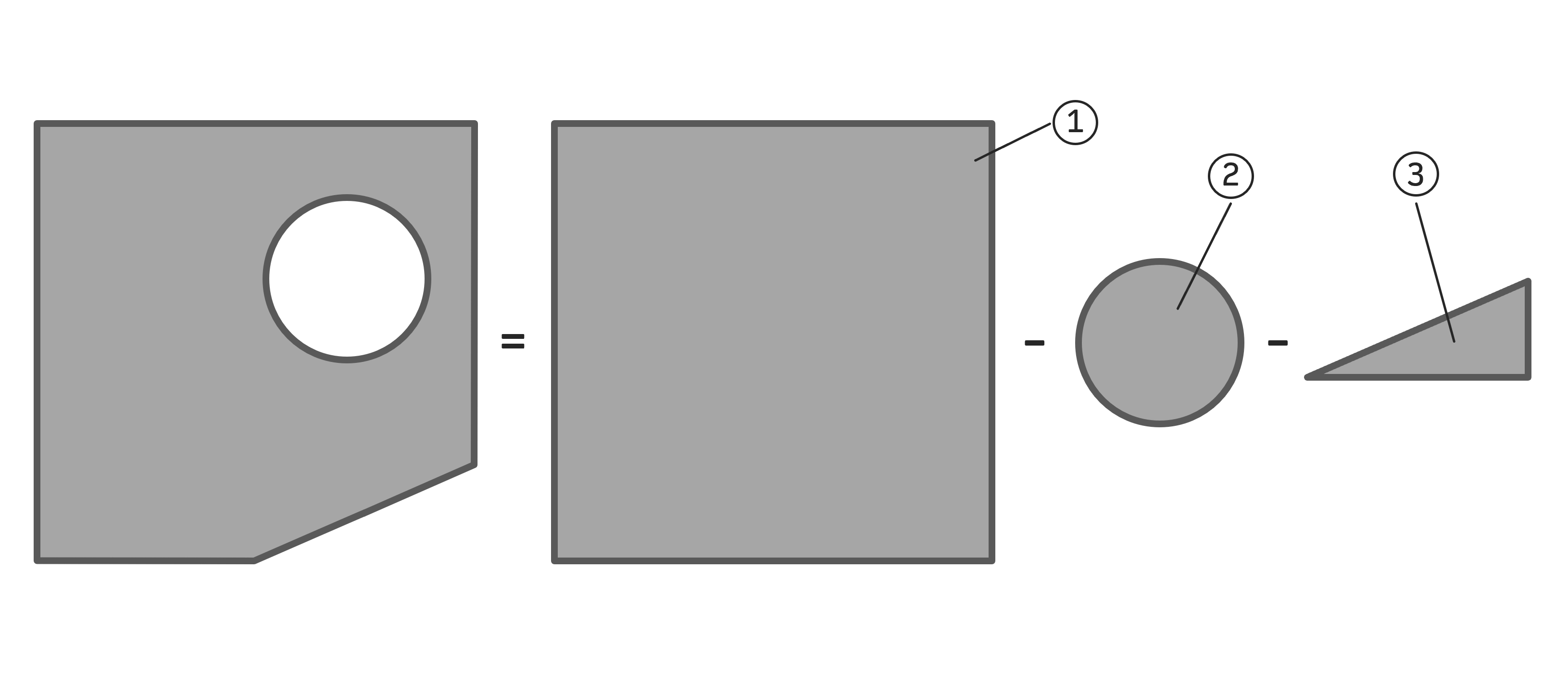
Grundsätzliches Vorgehen
Die zusammengesetzte Fläche besteht aus einem Quadrat \( 1 \), von dem ein Kreis \( 2 \) und ein Dreieck \( 3 \) rausgeschnitten wurden. Man rechnet daher ein Quadrat aus und zieht davon ein Dreieck und ein Kreis ab.
Schritt 2: Flächeninhalte und Einzelschwerpunkte bestimmen
Als nächstes müssen die Flächeninhalte \( A_1\,,A_2\,,A_3 \) und die Schwerpunkte der einzelnen Teilflächen \( S_1\,,S_2\,,S_3 \) bestimmt werden. Dazu wurden in der Abbildung die x- und y-Koordinaten der einzelnen Schwerpunkte markiert und für die folgenden Gleichungen abgelesen. Die Flächenschwerpunkte der einzelnen Teilflächen sind hier tabellarisch zusammengefasst.
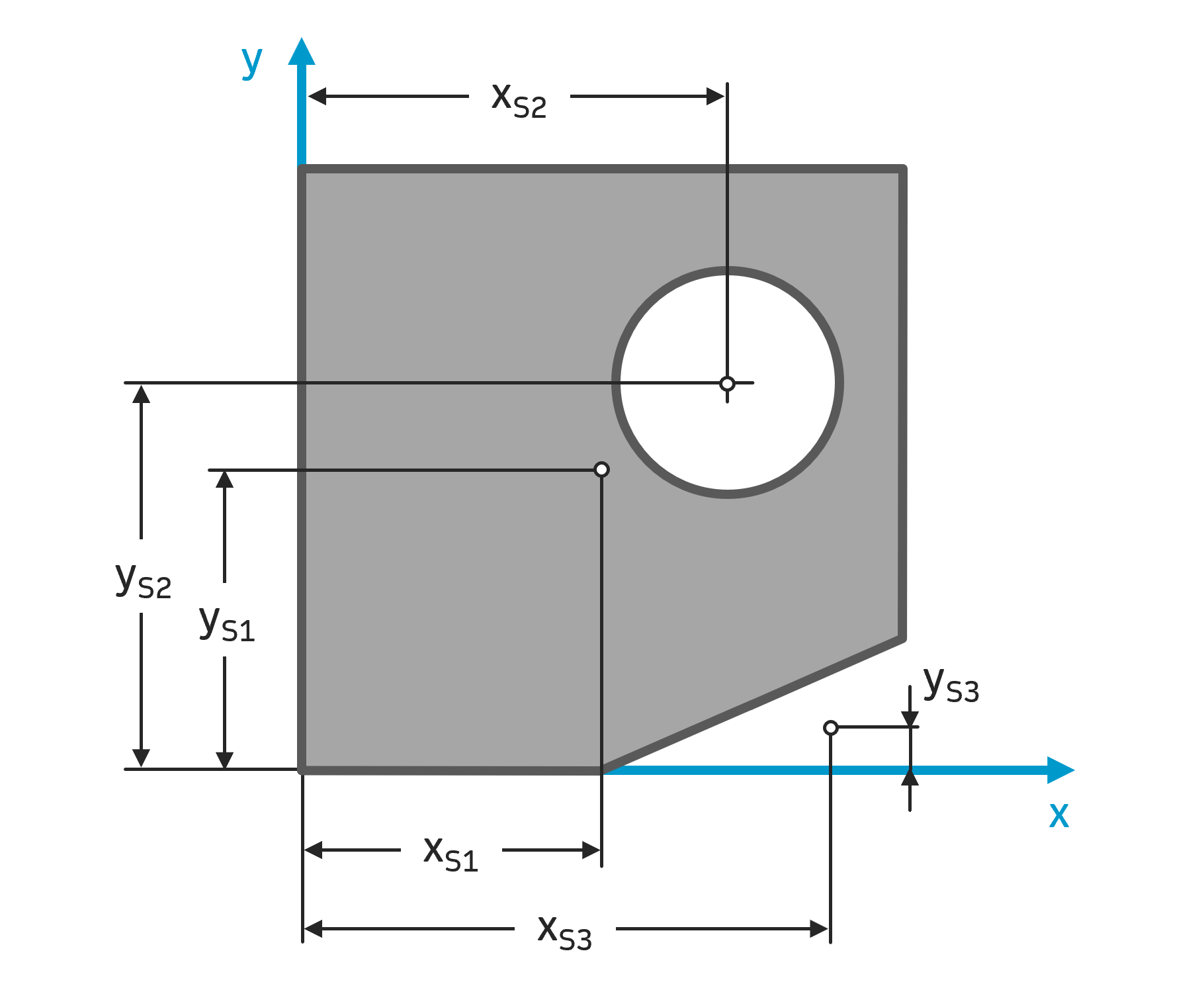
Die Koordinaten der einzelnen Flächen nach dem gegebenen Koordinatensystem sowie die Flächeninhalte sind:
Teilfläche 1: Quadrat
$$A_1 = 4a \cdot 4a = 16a^2$$ $$x_{S1}=2a$$ $$y_{S1}=2a$$
Teilfläche 2: Kreis
$$A_2 = -\pi a^2$$ $$x_{S2}=3a$$ $$y_{S2}=3a$$
Teilfläche 3: Dreieck
$$A_3 = -\frac{1}{2} \cdot 2a \cdot a = -a^2$$ $$x_{S3}=2a+ \frac{2}{3} \cdot 2a = \frac{10}{3}a$$ $$y_{S3} = \frac{1}{3} \cdot a = \frac{a}{3}$$
Negative Flächen
Flächen, die subtrahiert bzw. abgeschnitten werden, sind negativ. Deswegen haben die Teilflächen \( A_2 \) und \( A_3 \) ein negatives Vorzeichen.
Schritt 3a: Einsetzen in die Formel (Schwerpunkt berechnen)
Im letzten Schritt werden die Flächeninhalte und Einzelschwerpunkte vom vorherigen Schritt in die Formeln eingesetzt, um die Gesamtschwerpunkte zu bestimmen. Die Lage des Schwerpunktes lässt sich mit diesen Formeln berechnen:
$$x_S = \frac{\sum A_i \cdot x_{Si}}{\sum A_i}$$ $$y_S = \frac{\sum A_i \cdot y_{Si}}{\sum A_i}$$
Zuerst wird die x-Koordinate des Gesamtschwerpunkts bestimmt:
$$x_S = \frac{ A_1 \cdot x_{S1} + A_2 \cdot x_{S2} + A_3 \cdot x_{S3}}{A_1 + A_2 + A_3}$$ $$x_S = \frac{ 16a^2 \cdot 2a -\pi a^2 \cdot 3a -a^2 \cdot \frac{10}{3}a }{16a^2 -\pi \cdot a^2 – a^2}$$ $$x_S \approx 1,62 a$$
Und anschließend die y-Koordinate des Gesamtschwerpunkts:
$$y_S = \frac{ A_1 \cdot y_{S1} + A_2 \cdot y_{S2} + A_3 \cdot y_{S3}}{A_1 + A_2 + A_3}$$ $$y_S = \frac{ 16a^2 \cdot 2a -\pi a^2 \cdot 3a -a^2 \cdot \frac{a}{3} }{16a^2 -\pi \cdot a^2 – a^2}$$ $$y_S \approx 1,88 a$$
Wenn man jetzt noch zusätzlich die gegebene Seitenlänge \( a=10\,cm \) einsetzt, erhält man für die Lage des Schwerpunkts zahlenmäßig:
$$x_S = 16,2\,cm$$ $$y_S = 18,8\,cm$$
Schritt 3b: Schwerpunkt berechnen mithilfe der Tabelle
Alternativ kann man auch den Schwerpunkt mit dem Tabellenverfahren bestimmen. Man stellt dafür folgende Tabelle auf und füllt sie schrittweise mit den Flächen und den Koordinaten der einzelnen Flächenschwerpunkte, die in den Schritten zuvor bestimmt worden sind:
\[
\begin{array}{|c|c|c|}
\hline
\text{\( i \)} & \text{\( A_i \)} & \text{\( x_{Si} \)} & \text{\( y_{Si} \)} & \text{\( A_i \cdot x_{Si} \)} & \text{\( A_i \cdot y_{Si} \)} \\
\hline
1 & \text{\( 16a^2 \)} & \text{\( 2a \)} & \text{\( 2a \)} & \text{\( 32a^3 \)} & \text{\( 32a^3 \)} \\
\hline
2 & \text{\( -\pi a^2 \)} & \text{\( 3a \)} & \text{\( 3a \)} & \text{\( -3 \pi a^3 \)} & \text{\( -3 \pi a^3 \)} \\
\hline
3 & \text{\( -a^2 \)} & \text{\( \frac{10}{3} a \)} & \text{\( \frac{a}{3} \)} & \text{\( -\frac{10}{3} a^3 \)} & \text{\( -\frac{1}{3} a^3 \)} \\
\hline
\sum & \text{\( \approx 11,86 a^2 \)} & \text{-} & \text{-} & \text{\( \approx 19,24a^3 \)} & \text{\( \approx 22,24a^3 \)} \\
\hline
\end{array}
\]
Die Schwerpunktkoordinaten erhält man, indem man wiederum in die Formeln einsetzt:
$$x_S = \frac{\sum A_i \cdot x_{Si}}{\sum A_i} = \frac{19,24a^3}{11,86a^2} \approx 1,62a$$ $$y_S = \frac{\sum A_i \cdot y_{Si}}{\sum A_i} = \frac{22,24a^3}{11,86a^2} \approx 1,88a$$
Ist das Tabellenverfahren besser?
Das Tabellenverfahren spart oft keine Arbeit. Auch wenn es hier so aussieht, als ob die Berechnung des Schwerpunktes mit der Tabelle deutlich kürzer ist. Immerhin müssen ja die Flächeninhalte und die Schwerpunkte der Teilflächen genauso berechnet und abgelesen werden, wie es hier in Schritt 2 gemacht wurde. Ein weiterer großer Nachteil ist, dass viele Zahlen dicht beieinander stehen. Da sind Flüchtigkeitsfehler in der Klausur schon vorprogrammiert (Verrutschen der Zeilen/Spalten usw.). Oft wird versucht in der Tabelle selbst die Flächen oder sogar die Produkte \( A_i \cdot x_{Si} \) und \( A_i \cdot y_{Si} \) auszurechnen, obwohl das in einer Nebenrechnung außerhalb der Tabelle gemacht werden sollte. Aus diesen Gründen rate ich lieber dazu, die Schwerpunkte wie in den Schritten 2 und 3a zu berechnen.
Zusammenfassung: Schwerpunkt berechnen
- Flächen erkennen und nummerieren
- Flächeninhalte und Schwerpunkte der einzelnen Flächen berechnen
- In die Formeln für den Gesamtschwerpunkt einsetzen
$$x_S = \frac{\sum A_i \cdot x_{Si}}{\sum A_i}$$ $$y_S = \frac{\sum A_i \cdot y_{Si}}{\sum A_i}$$
Ergebnisse überprüfen
Zum Schluss lohnt es sich einen Blick auf die berechnete Lage des Schwerpunktes zu werfen. Immerhin kann man sich hier auf seine Intuition verlassen, um zu sagen, ob der Schwerpunkt richtig oder falsch berechnet wurde.
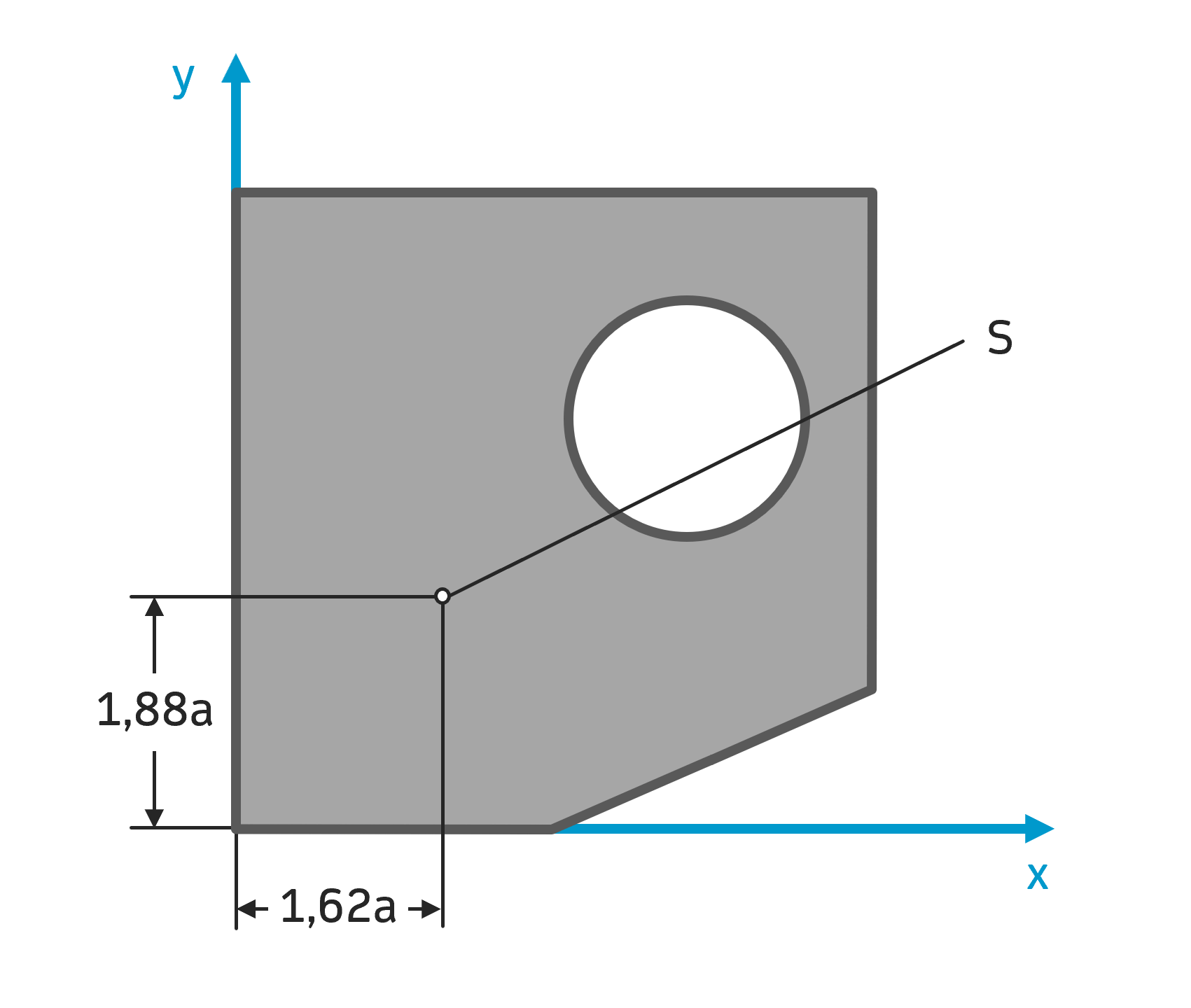
Versucht man eine Gabel mit seiner Fingerkuppe zu balancieren, dann tut man dies, indem man seinen Finger unterhalb des Schwerpunktes der Gabel positioniert. In der technischen Mechanik ist dies nicht anders: Die Lage des Flächenschwerpunktes ist dort, wo man seinen Finger platzieren müsste, um die Fläche zu balancieren. Insofern ist der berechnete Flächenschwerpunkt in diesem Fall tatsächlich plausibel, weil man dort seinen Finger platzieren würde, um die Fläche in Balance zu bringen. Mit dieser Erkenntnis kann man natürlich keine genauen Schwerpunktkoordinaten berechnen. Aber man kann damit zumindest prüfen, ob man sich nicht total verrechnet hat. Denn: Befindet sich der berechnete Flächenschwerpunkt nicht dort wo man es intuitiv erwartet, dann hat man sich (vielleicht) verrechnet.
Video: Schwerpunkt berechnen
In diesem Video wird Schritt für Schritt erklärt, wie der Schwerpunkt einer zusammengesetzten Fläche berechnet wird (mit und ohne das Tabellenverfahren).
Verwandte Themen
Flächenschwerpunkt: Überblick und Formeln
Lagerkräfte berechnen: Prüfungsaufgabe
Oder zurück zur Themenübersicht: Technische Mechanik 1