Technische Mechanik 1
In diesem Kurs einschreiben, um auf die Inhalte zugreifen zu können.
Kursinhalte
Alles ausklappen
Grundbegriffe
6 Themen
|
1 Test
ausklappen
Inhaltsübersicht
0% abgeschlossen
0/6 Einheiten
Zentrales Kräftesystem
5 Themen
|
1 Test
ausklappen
Allgemeines Kräftesystem
4 Themen
|
1 Test
ausklappen
Inhaltsübersicht
0% abgeschlossen
0/4 Einheiten
Schwerpunkte
4 Themen
|
1 Test
ausklappen
Inhaltsübersicht
0% abgeschlossen
0/4 Einheiten
Lagerreaktionen
6 Themen
|
1 Test
ausklappen
Inhaltsübersicht
0% abgeschlossen
0/6 Einheiten
Fachwerke
6 Themen
|
1 Test
ausklappen
Inhaltsübersicht
0% abgeschlossen
0/6 Einheiten
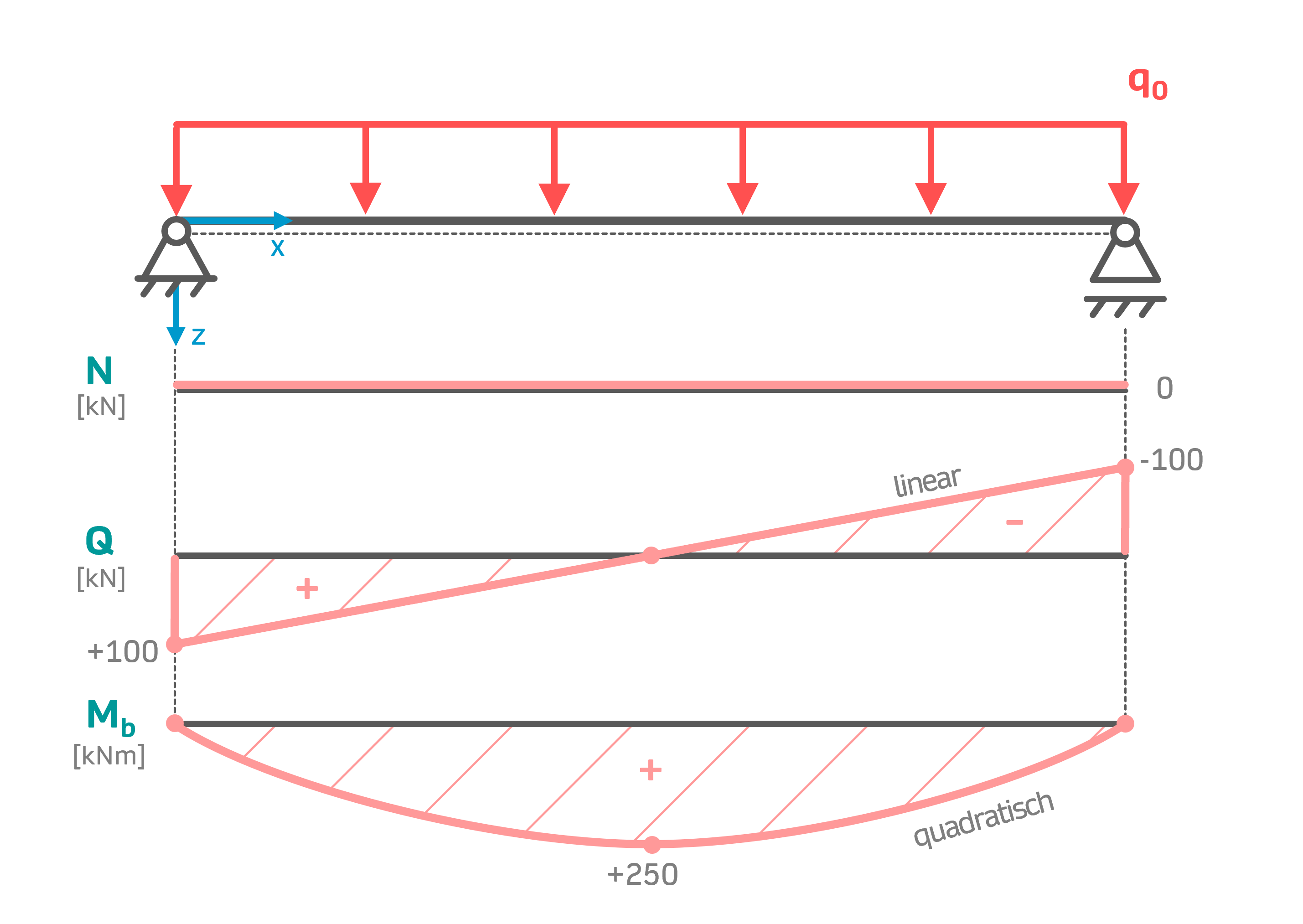
Schnittgrößen
5 Themen
|
1 Test
ausklappen
Inhaltsübersicht
0% abgeschlossen
0/5 Einheiten
Haftung und Reibung
2 Themen
|
1 Test
ausklappen
Inhaltsübersicht
0% abgeschlossen
0/2 Einheiten