Flächenträgheitsmoment berechnen (Beispielaufgabe)
Auf dieser Seite wird anhand einer Übungsaufgabe schrittweise erklärt, wie man bei einer zusammengesetzten Fläche das Flächenträgheitsmoment berechnen kann. Es wird das axiale Flächenträgheitsmoment \( I_y \) und \( I_z \) bei einem L-förmigen Querschnitt bestimmt.
Was ist das Flächenträgheitsmoment?
Das Flächenträgheitsmoment (auch Flächenmoment 2. Grades genannt) ist eine Größe, die sagt, wie sehr sich ein Querschnitt einer Biegeverformung widersetzen kann. Je größer das Flächenträgheitsmoment ist, desto größer ist der Widerstand dieses Querschnitts gegenüber einer Biegeverformung.
Aufgabenstellung: Flächenträgheitsmoment
Für den dargestellten L-förmigen Querschnitt (Winkelprofil) sind die Flächenträgheitsmomente \( I_y \) und \( I_z \) zu bestimmen. Es ist das vorgegebene y-z-Koordinatensystem zu verwenden, das seinen Koordinatenursprung im Gesamtschwerpunkt \( S \) des Querschnitts hat. Um welche Achse soll der Querschnitt belastet werden, um eine möglichst hohe Festigkeit zu gewährleisten?
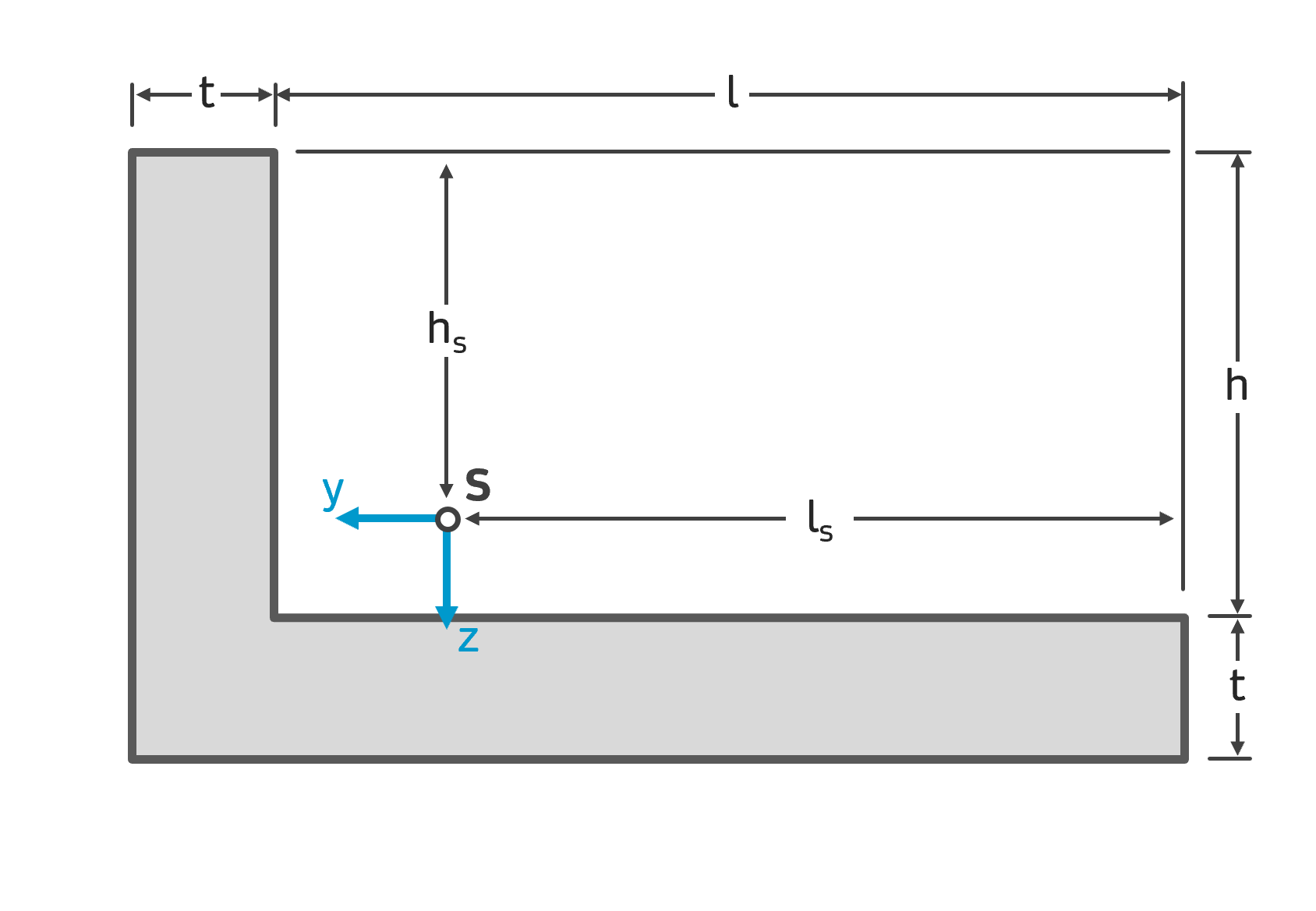
Gegeben: \( l=30\,cm \), \( h=18\,cm \), \( t=2\,cm \), \( h_s=15,4\,cm \), \( l_s=21,4\,cm \)
Lösung: Flächenträgheitsmoment berechnen
Schritt 1: Teilflächen erkennen und nummerieren
Da sich der Querschnitt aus mehreren Teilflächen zusammensetzt, sind im ersten Schritt die korrekten Teilflächen zu identifizieren. In den meisten Fällen setzt sich der Querschnitt aus einem Rechteck, einem Dreieck oder einem Kreis zusammen. Die Tabelle mit den Flächenträgheitsmomenten der wichtigsten Flächen kann helfen, die Teilflächen richtig zu identifizieren.
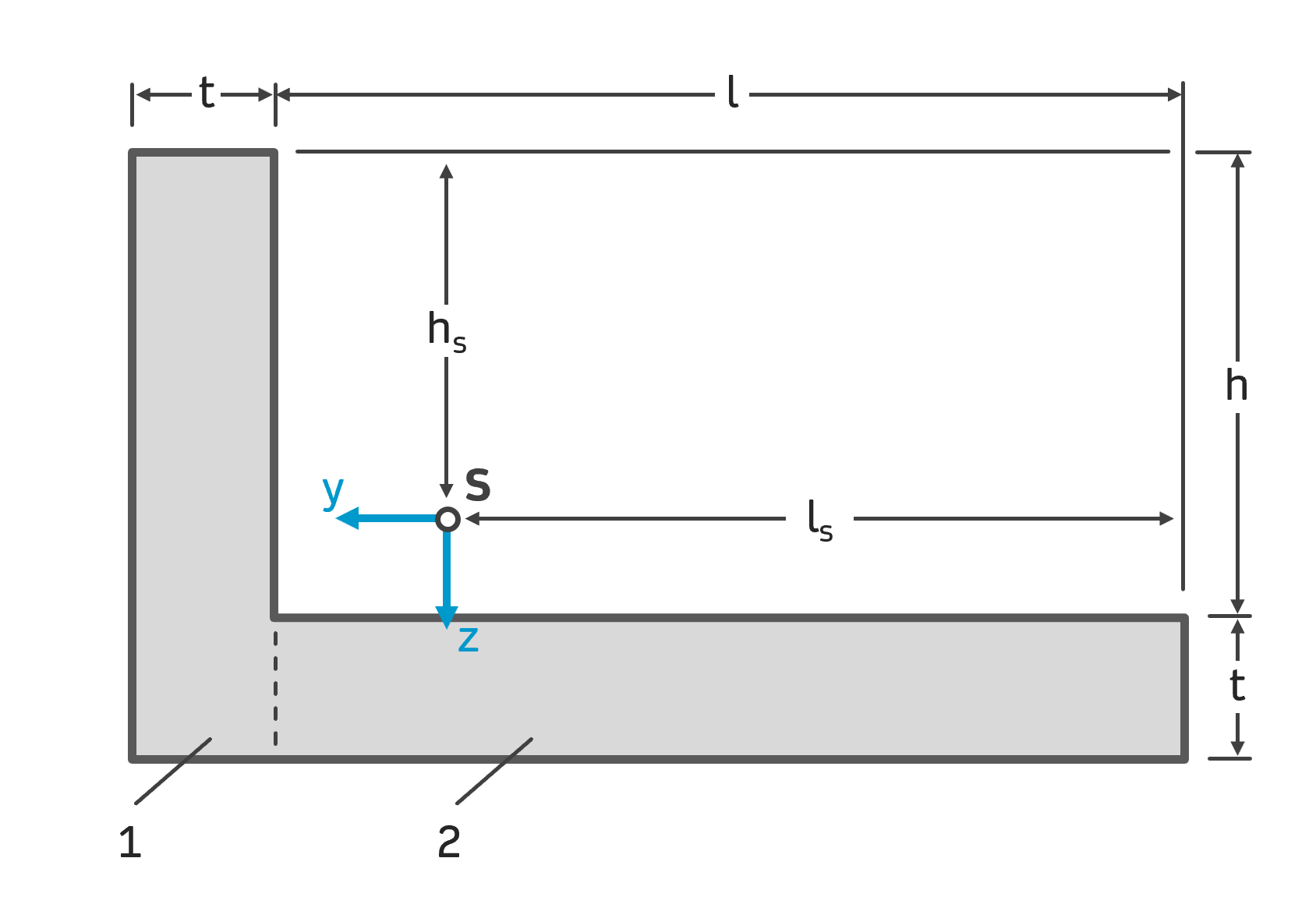
Das gegebene Winkelprofil wird so unterteilt, dass wir 2 Rechtecke bzw. rechteckige Streifen erhalten. Man kann aber auch den Querschnitt anders unterteilen. Folgende Unterteilung wäre ebenso denkbar: Ein großes Rechteck mit der Breite \( t+l \) und der Höhe \( t+h \). Davon wird der Hohlraum (kleines Rechteck) mit der Breite \( l \) und der Höhe \( h \) abgezogen. Wir arbeiten aber mit der Variante mit den beiden rechteckigen Streifen weiter.
Schritt 2: Schwerpunkt berechnen
Als nächstes müssen wir den Flächenschwerpunkt bestimmen. Das ist wichtig, um das Flächenträgheitsmoment bestimmen zu können. Es wird nämlich benötigt, um die Abstände für den Steiner-Anteil (Satz von Steiner) zu ermitteln. In manchen Fällen ist der Schwerpunkt bekannt, weil der Querschnitt entweder symmetrisch ist oder weil der Schwerpunkt bereits in der Aufgabenstellung gegeben ist. In diesem Rechenbeispiel ist die Lage des Schwerpunkts bereits bekannt, da sie in der Aufgabenstellung gegeben ist. Zur Erinnerung, der Schwerpunkt hat (von der rechten oberen Ecke aus gezählt) die folgenden Koordinaten:
$$ h_s=15,4\,cm $$ $$ l_s=21,4\,cm $$
Nichtsdestotrotz: Wäre der Schwerpunkt nicht bekannt, müsste er jetzt an dieser Stelle berechnet werden. Die Tabelle der Schwerpunkte und ein Rechenbeispiel (Schwerpunkt berechnen) zeigen nochmal ausführlich, wie man den Schwerpunkt bestimmt.
Schritt 3a: Flächenträgheitsmoment berechnen bzgl. y-Achse
Wir berechnen zunächst das Flächenträgheitsmoment \( I_y \). Bei zusammengesetzten Teilflächen lässt sich das Flächenträgheitsmoment mit folgender Formel berechnen:
$$ I_y = \sum I_{y,i} + \sum A_i \cdot b_i^2 $$
Der Ausdruck \( \sum I_{y,i} \) steht für die Flächenträgheitsmomente der einzelnen Teilflächen. Hier setzt man die Formeln aus der Tabelle mit den Flächenträgheitsmomenten ein. Der nachfolgende Ausdruck \( \sum A_i \cdot b_i^2 \) steht für den Steiner-Anteil (Satz von Steiner). Für den Steiner-Anteil benötigt man nur den Flächeninhalt und einen Abstand auf den wir gleich eingehen werden. Wir schreiben aber zunächst die Formel für das Flächenträgheitsmoment ohne Summenzeichen auf. Dann sieht sie nämlich viel verständlicher aus:
$$ I_y = I_{y1} + I_{y2} + A_1 \cdot b_1^2 + A_2 \cdot b_2^2 $$
Wir bestimmen nun nacheinander die einzelnen Größen. Die Flächenträgheitsmomente
$$ I_{y1} = \frac{t \cdot (h+t)^3}{12} \approx 1333,3\,cm^4 $$ $$ I_{y2} = \frac{l \cdot t^3}{12} = 20\,cm^4 $$
für die Teilflächen 1 und 2 ergeben sich mithilfe der Tabelle. Hier handelt es sich jeweils um ein Rechteck. Man muss an dieser Stelle lediglich beachten, welche Seitenlänge des Rechtecks hoch drei gerechnet wird. Es ist stets die Seitenlänge, die senkrecht zur Biegeachse steht. Die Flächeninhalte
$$ A_1 = t \cdot (h+t) = 40\,cm^2 $$ $$ A_2 = l \cdot t = 60\,cm^2 $$
der beiden rechteckigen Teilflächen lassen sich ganz leicht bestimmen. Die Formel für den Flächeninhalt eines Rechtecks sowie für andere Flächen sind hier zu finden: Schwerpunkte von Flächen und deren Flächeninhalte. Jetzt fehlen nur noch die Abstände \( b_1 \) und \( b_2 \) für den Steiner-Anteil.
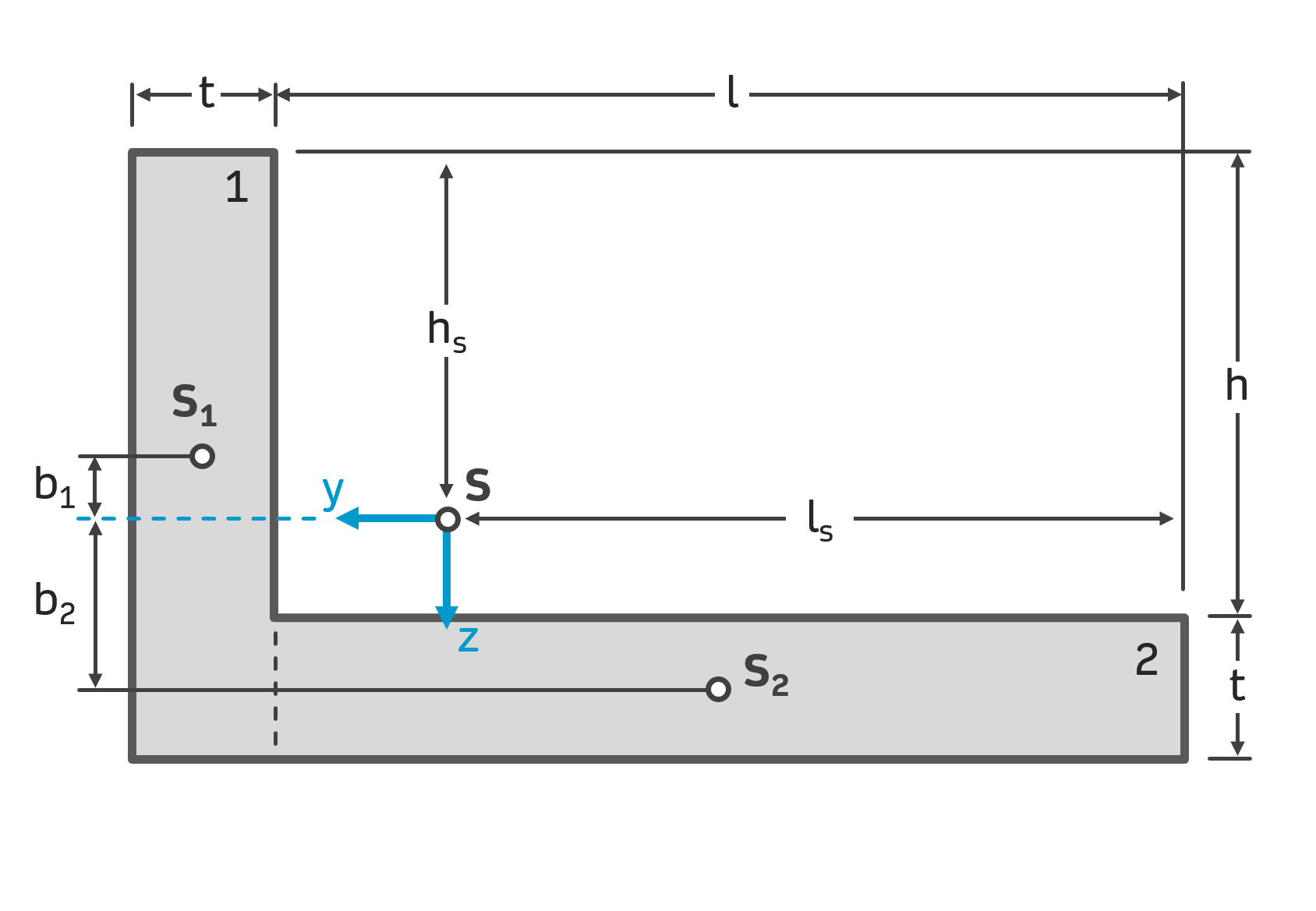
Die sogenannten Steiner-Abstände sagen aus, wie weit der Teilflächenschwerpunkt von der Biegeachse entfernt ist. Die Biegeachse ist in diesem Fall die y-Achse und verläuft stets durch den Gesamtschwerpunkt. Um die Abstände \( b_1 \) und \( b_2 \) zu bestimmen, ergänzen wir in der Skizze zwei Maße, die uns das Ablesen der Steiner-Abstände erleichtern.
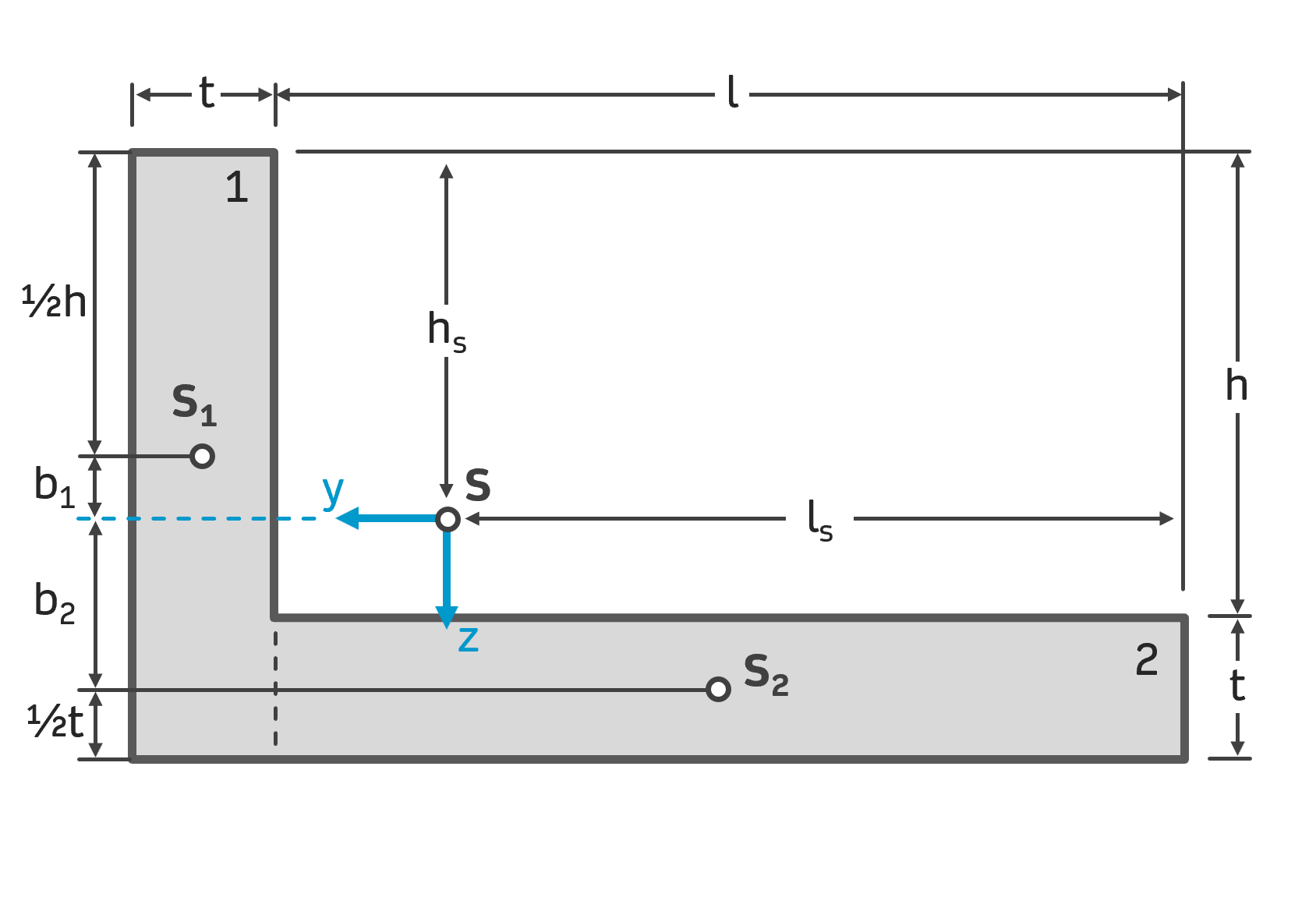
Nun kann man ganz leicht erkennen, dass
$$ h_s = \frac{h}{2} + b_1 $$ $$ \Rightarrow b_1 = h_s – \frac{h}{2} = 6,4\,cm $$
gilt. Den anderen Abstand des Steiner-Anteils erhält man folgendermaßen:
$$ h_s + b_2 + \frac{t}{2} = h + t $$ $$ \Rightarrow b_2 = h + t – h_s – \frac{t}{2} = 3,6\,cm $$
Nun müssen wir die einzelnen Werte nur noch in die Formel einsetzen:
$$ I_y = I_{y1} + I_{y2} + A_1 \cdot b_1^2 + A_2 \cdot b_2^2 $$ $$ I_y = 1333,3 + 20 + 40 \cdot 6,4^2 + 60 \cdot 3,6^2 $$ $$ I_y \approx 3769,3\,cm^4 $$
Und so erhält man das gesuchte Flächenträgheitsmoment \( I_y \). Der Einfachheit halber wurden die Einheiten nicht mit eingesetzt. Das ist aber kein Problem, denn alle Größen sind in \( cm \) gegeben. Wie man das Flächenträgheitsmoment \( I_z \) bestimmt, erfahren wir im nächsten Abschnitt.
Schritt 3b: Flächenträgheitsmoment berechnen bzgl. z-Achse
Das Flächenträgheitsmoment \( I_z \) bezüglich der z-Achse lässt sich fast wie zuvor berechnen. Die Formel für \( I_z \) lautet:
$$ I_z = \sum I_{z,i} + \sum A_i \cdot a_i^2 $$
Schreiben wir die Summenzeichen aus, sieht der Ausdruck viel besser aus:
$$ I_z = I_{z1} + I_{z2} + A_1 \cdot a_1^2 + A_2 \cdot a_2^2 $$
Wir gehen ähnlich vor wie im vorherigen Abschnitt und bestimmen mithilfe der Tabelle zuerst die Flächenträgheitsmomente der einzelnen (rechteckigen) Teilflächen 1 und 2:
$$ I_{z1} = \frac{t^3 \cdot (h+t)}{12} = 12\,cm^4 $$ $$ I_{z2} = \frac{l^3 \cdot t}{12} = 4500\,cm^4 $$
Da diesmal die z-Achse unsere Biegeachse ist, wird die Seitenlänge hoch drei genommen, die senkrecht zur z-Achse steht. Die Flächeninhalte \( A_1 \) und \( A_2 \) sind schon vom vorherigen Abschnitt bekannt. Wir kommen daher direkt zu den Abständen des Steiner-Anteils. Wie eingangs erwähnt, handelt es sich um den Abstand zwischen dem Teilflächenschwerpunkt und der Biegeachse. Daraus ergeben sich die in der Skizze eingezeichneten Abstände \( a_1 \) und \( a_2 \).
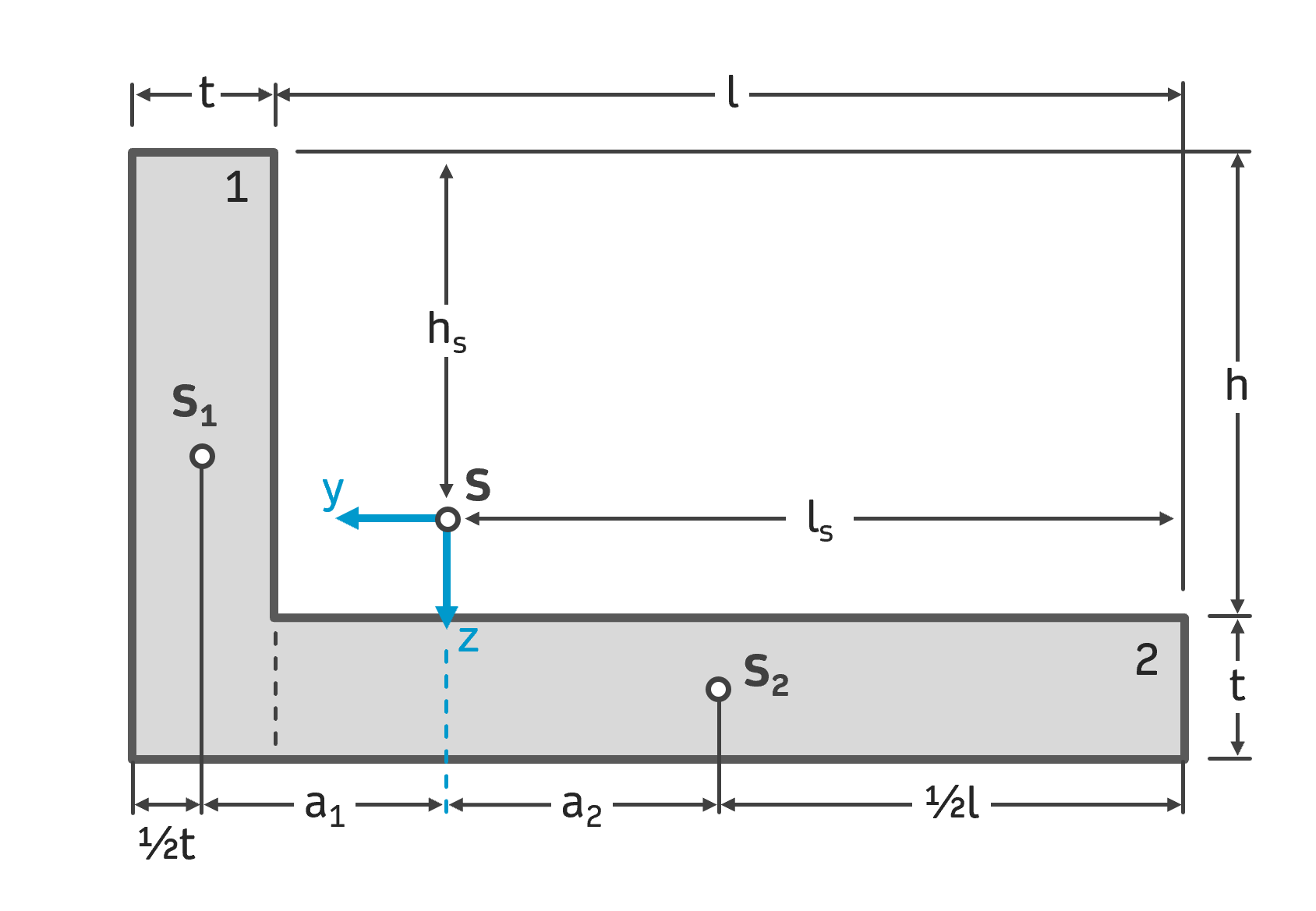
Mithilfe der eingezeichneten Längen lässt sich schnell erkennen, dass
$$ l_s = \frac{l}{2} + a_2 $$ $$ \Rightarrow a_2 = l_s – \frac{l}{2} = 6,4\,cm $$
gilt. Den anderen Abstand für den Steiner-Anteil erhält man wie folgt:
$$ l+t = l_s + a_1 + \frac{t}{2} $$ $$ \Rightarrow a_1 = l + t – l_s – \frac{t}{2} = 9,6\,cm $$
Da nun alle Werte bekannt sind, können wir einsetzen:
$$ I_z = I_{z1} + I_{z2} + A_1 \cdot a_1^2 + A_2 \cdot a_2^2 $$ $$ I_z = 12 + 4500 + 40 \cdot 9,6^2 + 60 \cdot 6,4^2 $$ $$ I_z = 10656\,cm^4 $$
So kommt man schließlich auf das Flächenträgheitsmoment \( I_z \).
Auswertung der Ergebnisse
Die Berechnung hat uns folgende Flächenträgheitsmomente geliefert:
$$I_y \approx 3769,3\,cm^4$$ $$I_z = 10656\,cm^4$$
Das Flächenträgheitsmoment \( I_z \) ist fast drei mal so groß wie das Flächenträgheitsmoment \( I_y \). Bei dem gegebenen L-förmigen Querschnitt wäre es daher ratsam, die Belastungen so einzuleiten, dass der Balken möglichst um die z-Achse gebogen wird, da der Querschnitt auf diese Art fast drei mal „stärker“ ist als bei Biegung um die y-Achse.
Zusammenfassung
Das Flächenträgheitsmoment \( I_y \) bzw. \( I_z \) eines zusammengesetzten Querschnitts kann im Normalfall mit folgender Anleitung berechnet werden:
- Teilflächen erkennen und nummerieren
- Gesamtschwerpunkt bestimmen (falls nicht bekannt)
- Flächenträgheitsmoment für Teilflächen einzeln bestimmen
- Abstand für den Steiner-Anteil ablesen
- Einsetzen in die Formel: \( I_y = \sum I_{y,i} + \sum A_i \cdot b_i^2 \)
Die Flächenträgheitsmomente für die einzelnen Teilflächen kann mit der Tabelle der Flächenträgheitsmomente bestimmt werden. Bei den Abständen für den Steiner-Anteil muss beachtet werden, dass damit die Abstände vom Teilflächenschwerpunkt bis zur Biegeachse gemeint sind. Die Biegeachse erkennt man an dem Index y oder z – je nachdem ob man \( I_y \) oder \( I_z \) berechnet. Im Normalfall geht die Biegeachse durch den Schwerpunkt des Querschnitts durch. Für das Flächenträgheitsmoment \( I_z \) geht man analog vor.
FAQ: Flächenträgheitsmoment berechnen
Gibt es neben dem Flächenträgheitsmoment noch etwas, das den Biegewiderstand beeinflusst?
Ausgezeichnete Frage! Ja, es gibt noch etwas. Neben dem Flächenträgheitsmoment gibt es noch den E-Modul (Elastizitätsmodul), das den Widerstand eines Körpers gegen Biegeverformung ausmacht. Ein Körper ist schließlich widerstandsfähiger, wenn erstens der Querschnitt stärker bzw. dicker ist und zweitens der Werkstoff „gut“ bzw. eine hohe Festigkeit hat.
Kann das Flächenträgheitsmoment negativ werden?
Nein, denn: Das Flächenträgheitsmoment sagt aus, wie sehr ein Querschnitt bei Biegung nachgibt. Jeder Körper bzw. jeder Querschnitt leistet bei Biegung Widerstand. Ein negatives Flächenträgheitsmoment würde bedeuten, dass der Querschnitt keinen Widerstand leistet sondern im Gegenteil: Der Querschnitt unterstützt die Biegung. Und das ist natürlich ausgeschlossen.
Was ist der Satz von Steiner?
Der Satz von Steiner sagt aus, dass Teilflächen, die weiter vom Gesamtschwerpunkt entfernt sind, mehr Widerstand gegen Biegung leisten als Flächen, die näher am Gesamtschwerpunkt sind. Das erkennt man auch gut an dem Steiner-Anteil: \( \sum A_i \cdot b_i^2 \). Je größer der Abstand \( b_i \) ist, desto größer der Steiner-Anteil und desto größer das Flächenträgheitsmoment. In diesem Fall wächst genau genommen das Flächenträgheitsmoment mit dem Quadrat des Abstands an, da der Steiner-Abstand nicht einfach in die Gleichung eingeht, sondern quadratisch.
Video: Flächenschwerpunkt bestimmen (Steiner-Anteil)
Bei zusammengesetzten Querschnitten muss der Steiner-Anteil berechnet werden. Dafür muss man wissen, wo sich der Schwerpunkt einer Fläche befindet. Dieses Video zeigt ausführlich, wie der Flächenschwerpunkt eines Querschnitts berechnet wird.
Verwandte Themen
Flächenträgheitsmomente: Tabelle und Formeln
Schwerpunkt einer Fläche berechnen (Beispielaufgabe)

